The fourier transform of d(t) is 1. ∫ −= ) δω ω()exp( ) exp( [0]) 1titdt i ∞ −∞ ∫ −=−= t d(t) w!
Draw A Sketch Of The Fourier Transform Terms, Using our fourier transform we can calculate the sine and cosine coefficients that give us the speed and size of connected circles that would imitate our drawing. As revision, i am going through signals and systems, and in section 7.1the authors are sketching representative spectra for x (t) and xp (t) as follows. Sine and cosine waves can make other functions!
Use the slider to change the amount of coefficients calculated. F(t)= 1 2π f(ω)eiωt −∞ ∞ ∫dω f(ω)=f(t)e−iωt −∞ ∞ ∫dt (6.50) here f(t) is some real time series in the independent variable t, and f(ω) is the fourier transform of f(t), and is generally a complex number with a. Discrete fourier transform (dft) recall the dtft: Sine and cosine waves can make other functions!
myFourierEpicycles draw your own fourier epicycles.
Sketch magnitude and phase of fourier transform of h(t). A finite signal measured at n. Dtft is not suitable for dsp applications because •in dsp, we are able to compute the spectrum only at specific discrete values of ω, •any signal in any dsp application can be measured only in a finite number of points. F = f (f) let f 1 denote the inverse fourier transform: % the coordinates of the curve you want to draw must be saved in.mat beforehand. Using this we can find c3 and c4 as samuel the other poster has shown.

Patent US6963891 Fast fourier transform Google Patentsuche, Here we see that adding two different sine waves make a new wave: For example, if you wanted to draw a circle you would say f ( t) = e 2 π i t. My guess is that it will look something like this in the first 3 terms: Fourier transform is purely imaginary. X(ω) = x∞ n=−∞ x(n)e−jωn.

Fourier Series Examples, First, apply the the convolution theorem: E ect of windowing on fourier representations step 2: Uses the discrete fourier transform to draw an input signal. F ( ω) = f { f ( t) } = f { ( 2 c o s ( 400 t) + 4 s i n ( 500 t + π 3)) ⋅ c (.

3Blue1Brown But what is a Fourier series? From heat flow, Use the slider to change the amount of coefficients calculated. Examples, properties, common pairs properties: Here we see that adding two different sine waves make a new wave: Notation let f denote the fourier transform: You can again make you own drawing in the square, to see how the circles imitate it using fourier analysis.

Fourier Series, Using this we can find c3 and c4 as samuel the other poster has shown. The x coordinate is converted into a complex number with the real part and the y coordinate as the imaginary part. And also notice that it is periodic with period 2*pi. Draw a picture or sample one, press space, then watch an epic simulation of.

dft Formulas of the Fourier transform family Signal, I had quite a bit fun creating this, so at the end there is a brief explanation trying to give the reader some mathematical intuition as to how. The x coordinate is converted into a complex number with the real part and the y coordinate as the imaginary part. One hardly ever uses fourier sine and cosine transforms. X (jω).

Patent US20130046469 Diffuse reflectance infrared, Discrete fourier transform (dft) recall the dtft: A short tutorial video on how the fourier transform works. A finite signal measured at n. For example, if you wanted to draw a circle you would say f ( t) = e 2 π i t. Examples, properties, common pairs properties:

How to get Fourier coefficients to draw any shape using, Dtft is not suitable for dsp applications because •in dsp, we are able to compute the spectrum only at specific discrete values of ω, •any signal in any dsp application can be measured only in a finite number of points. Fourier transform is purely imaginary. Let x w [n]represent a windowed version of. The attempt at a solution i know.

Patent US4189214 Fourier transform lens system Google, One hardly ever uses fourier sine and cosine transforms. Examples, properties, common pairs properties: Draw a picture or sample one, press space, then watch an epic simulation of epicycles being drawned identically as your picture. Fourier transform is purely imaginary. X (s) = x (t) e −.

frequency approximation of a digital signal using the, And frequency, we can write the fourier transform pair as integrals: Examples, properties, common pairs properties: Show activity on this post. The x coordinate is converted into a complex number with the real part and the y coordinate as the imaginary part. Here we see that adding two different sine waves make a new wave:

draw Fourier Series Expansion with tikz/pgfplots TeX, E ect of windowing on fourier representations step 2: The video is designed for those who know what a fourier transform is but need to understand at a b. That is, a function f: Discrete fourier transform (dft) recall the dtft: First, apply the the convolution theorem:

Fourier Series Example, [ 0, 1] → c, that gives you a point in the complex plane for every input between o and 1. At this point half of the problem is solved, we have all the coefficients. First of all, you need to write whatever it is you want to draw as a curve in the complex plane. Drawing user drawings with.

But what is a Fourier series? From heat flow to drawing, Also some has convert scripts [in progress] to convert svg files into valid path I had quite a bit fun creating this, so at the end there is a brief explanation trying to give the reader some mathematical intuition as to how. The x coordinate is converted into a complex number with the real part and the y coordinate as.

Implementing Fourier transform as a Neural Network neeks, Here we see that adding two different sine waves make a new wave: F = f 1 (f ) the fourier transform: Using this we can find c3 and c4 as samuel the other poster has shown. Drawing user drawings with fourier transform by david snyder (source code) svg to fourier series in vanilla js by tayler miller (source code).

2nd Perspective Drawing Free download on ClipArtMag, Enter a function, play with the slider for l to sketch some of a functions fourier series. F = f (f) let f 1 denote the inverse fourier transform: Here we see that adding two different sine waves make a new wave: Discrete fourier transform (dft) recall the dtft: The video is designed for those who know what a fourier.

A Tale of Math & Art Creating the Fourier Series Harmonic, The normalized dft bin values are the fourier coefficients. in other words, simply replacing an integer n in the centered inverse dft with a continuous real valued variable will produce the interpolated results. Dt = x (s)| s = jω. Close all s = load(�r_zeta.mat�); X (jω) = x (t) e. F = f 1 (f ) the fourier transform:

Solved 2 Fourier Series (a) For The Continuoustime Perio, X(ω) = x∞ n=−∞ x(n)e−jωn. We are seeing the effect of adding sine or cosine functions. The x coordinate is converted into a complex number with the real part and the y coordinate as the imaginary part. Use the slider to change the amount of coefficients calculated. For example, if you wanted to draw a circle you would say f.
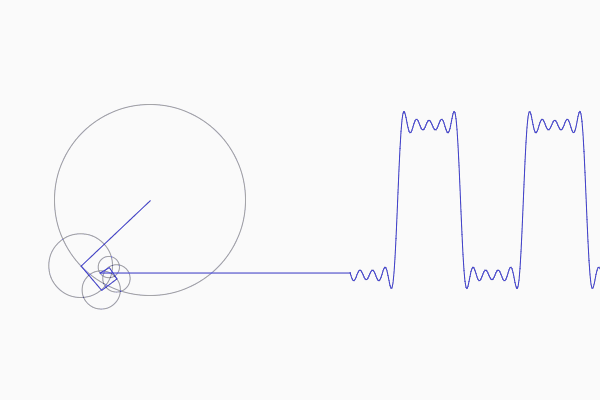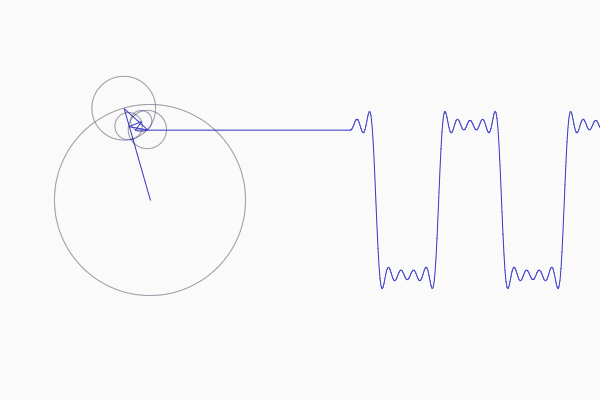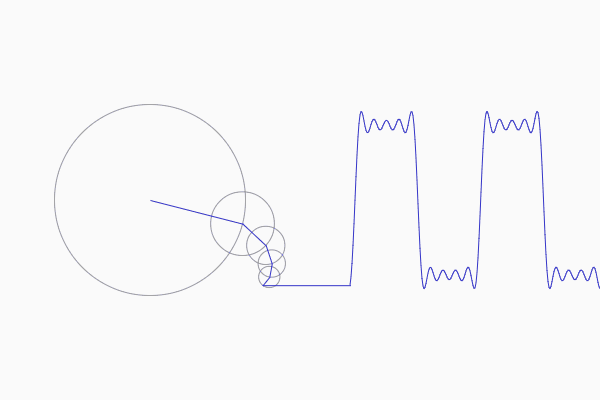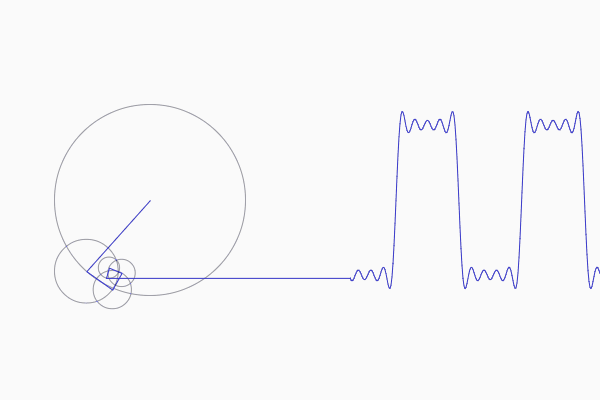
Why does the Fourier transform work? An intuition. by, Notation let f denote the fourier transform: This gui computes the required epicycles (i.e., radii, frequency and phase of all of them) in order to match a previously drawn curve, depicting an animation to see the result. The attempt at a solution i know that the magnitude 2 of h(f) is total power gain, so perhaps by taking the square.

Fourier Transform (FT) Questions and Answers in MRI, Close all s = load(�r_zeta.mat�); Use fourier transform to draw epicycles with your drawings. Fourier transform is purely imaginary. X w[n] = x[n]w[n] = ejωonw[n] then x w(ω) = x∞ n=−∞ ejωonw[n]e−jωn dtft analysis equation = x∞ n=−∞ w[n]e−jn combine exponential terms = w o) dtft of w[n], shifted in frequency Sine and cosine waves can make other functions!

Fourier Transform drawing (+source) YouTube, F = f (f) let f 1 denote the inverse fourier transform: Here we see that adding two different sine waves make a new wave: The function also allows for uploading the xy coordinates of a custom. X w[n] = x[n]w[n] = ejωonw[n] then x w(ω) = x∞ n=−∞ ejωonw[n]e−jωn dtft analysis equation = x∞ n=−∞ w[n]e−jn combine exponential terms.

PPT Chapter 15 Fourier Series and Fourier Transform 15.3, I had quite a bit fun creating this, so at the end there is a brief explanation trying to give the reader some mathematical intuition as to how. And also notice that it is periodic with period 2*pi. X (s) = x (t) e −. Use the slider to change the amount of coefficients calculated. % the coordinates of the.

Differential equations Fourier series, ∫ −= ) δω ω()exp( ) exp( [0]) 1titdt i ∞ −∞ ∫ −=−= t d(t) w! Using our fourier transform we can calculate the sine and cosine coefficients that give us the speed and size of connected circles that would imitate our drawing. The fourier series is infinite, you can only graph a partial sum of the series for.

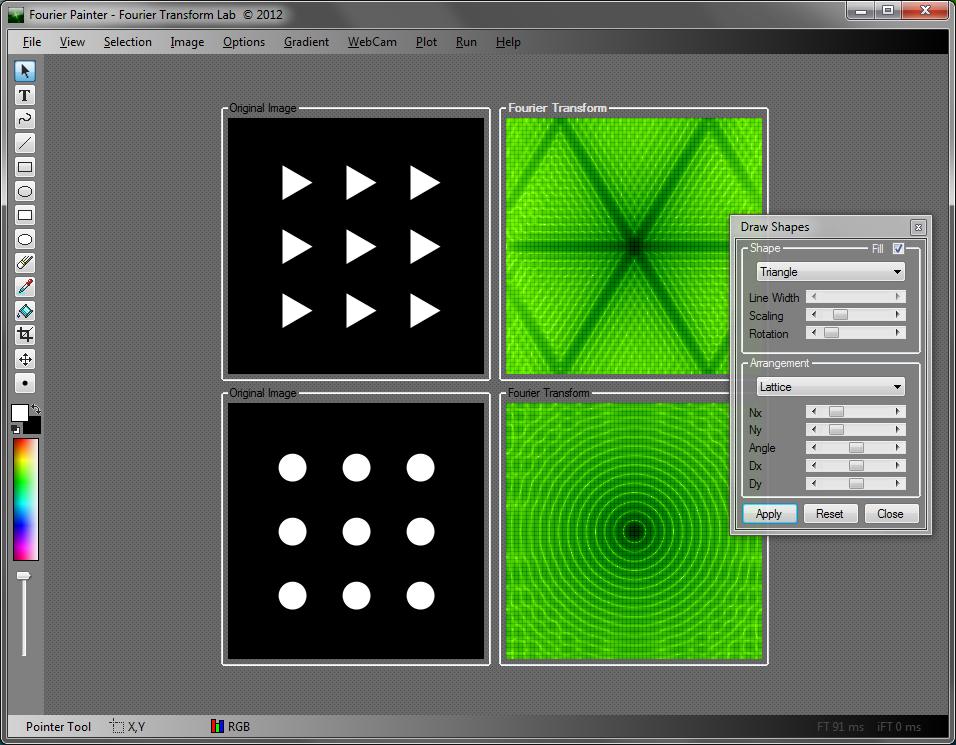
FourierPainter, Fourier Painter, 1D & 2D Fourier Transforms, E ect of windowing on fourier representations step 2: Here we see that adding two different sine waves make a new wave: Dtft is not suitable for dsp applications because •in dsp, we are able to compute the spectrum only at specific discrete values of ω, •any signal in any dsp application can be measured only in a finite number.

myFourierEpicycles draw your own fourier epicycles., Use fourier transform to draw epicycles with your drawings. Notation let f denote the fourier transform: F = f 1 (f ) the fourier transform: Let x w [n]represent a windowed version of. The x coordinate is converted into a complex number with the real part and the y coordinate as the imaginary part.

Fourier Transform of Alternating Periodic Rectangular, Examples, properties, common pairs properties: Close all s = load(�r_zeta.mat�); F (f + g ) = f (f)+ f (g ) We can write f˜(k)=f˜c(k)+if˜ s(k) (18) where f˜ s(k) is the fourier sine transform and f˜c(k) the fourier cosine transform. You can again make you own drawing in the square, to see how the circles imitate it using fourier.

Drawing anything with Fourier Series using Blender and Python, Sine and cosine waves can make other functions! And also notice that it is periodic with period 2*pi. ∫ −= ) δω ω()exp( ) exp( [0]) 1titdt i ∞ −∞ ∫ −=−= t d(t) w! 2d line art fourier transform animation contents. X(ω) = x∞ n=−∞ x(n)e−jωn.